Calculus is the mathematical study of change, akin to algebra’s concern with structure and geometry with space. It allows for the calculation of gradients, areas, and volumes through two main branches: Differential and Integral Calculus.
Understanding Calculus is essential for scientists, engineers, and economists as it serves as the foundation for much of modern mathematics and physics. Its applications are ubiquitous, ranging from computing the dynamics of celestial bodies to determining the optimal investment strategies in finance.
With its origins dating back to the works of Leibniz and Newton, Calculus remains a vital tool in tackling complex problems involving change and motion. Simplified, it breaks down daunting real-world problems into solvable equations. Its principles guide us in making predictions, optimizing systems, and understanding the world in mathematical terms. Precision in learning and applying Calculus can open doors to technological innovation and scientific breakthroughs, ensuring its enduring relevance in academia and industry alike.
Understanding The Basics Of Calculus
Calculus stands as a cornerstone of modern mathematics and science. Its concepts are crucial for solving complex problems in fields like engineering, physics, economics, and beyond. Getting to grips with the basics of calculus opens a world of understanding in professional and academic pursuits alike. Let’s dive into the fundamental aspects that shape the vast landscape of calculus.
Defining Calculus: Purpose And Foundations
Calculus serves as a tool for analyzing changes. Its main purpose is to understand movement and growth in various contexts. Through limits, derivatives, and integrals, calculus breaks down complex systems into understandable parts.
Differentiating Between Differential And Integral Calculus
These two branches of calculus, though distinct, complement each other. Differential calculus focuses on rates of change, while integral calculus deals with accumulation of quantities.
- Differential calculus: Involves finding the slope of a curve.
- Integral calculus: Concerns the total size or value, like area under a curve.
The Historical Evolution Of Calculus
The development of calculus was a game-changing moment in history. Not one, but two famed mathematicians, Isaac Newton and Gottfried Wilhelm Leibniz, independently developed the concepts of calculus in the 17th century. This period marked the beginning of detailed studies into motion and change leading to advancements in a variety of disciplines.
Key Concepts And Principles
Calculus unlocks the door to understanding the motion of objects, growth in nature, and many more real-world problems. This branch of mathematics revolves around three crucial ideas: limits, derivatives, and integrals. Mastery of these concepts provides the tools needed to analyze both static and dynamic systems.
Exploring Limits: Approaching Infinity
Limits in calculus help us understand values as they get incredibly large or small. Imagine a point on a graph that gets closer and closer to a line but never touches it. This is the essence of a limit. We use limits to define and understand behaviors in mathematics that would otherwise be hard to grasp.
Derivatives: Rates Of Change And Slopes Of Curves
The derivative is a measure of how a function changes as its input changes. Derivatives describe the slope of a curve at any point. Think of it as the speed of a car at a specific time. It tells us the rate at which one quantity changes with respect to another.
In simple terms:
- Instantaneous rate of change: How quickly something is changing at a single point.
- Slope of the tangent line: The tilt or steepness of a line just touching a curve.
Integrals: Accumulated Quantities And Areas Under Curves
While derivatives break functions down, integrals build them up. Integrals allow us to find the accumulated total of a quantity. Imagine adding up slices to find the area under a curve. This is how integrals connect to real life, like finding the total distance traveled by a car when you know its speed at all times.
Key points about integrals:
- Area under a curve: Total space between a curve and the x-axis.
- Accumulated quantity: A sum of values over a range, like total distance.
The Rules Of Differentiation
The Rules of Differentiation serve as the backbone of calculus, unlocking the secrets of rate, change, and slope. Understanding these rules helps solve complex problems with ease. Get ready to discover the magic behind these powerful mathematical tools!
Mechanics Of The Power Rule
The Power Rule is the simplest yet most powerful rule for differentiation. It’s the go-to technique for finding derivatives of functions with powers. Here’s a quick guide:
- Identify the exponent in your function.
- Multiply the coefficient by the exponent.
- Decrease the exponent by one.
The formula looks like this: d/dx [x^n] = nx^(n-1).
Product And Quotient Rules: Derivatives Of Multiplication And Division
When two functions multiply, the Product Rule springs into action. It allows the differentiation of a function that is the product of two other functions. The formula is:
(f(x) g(x))’ = f’(x) g(x) + f(x) g’(x)
Division brings in the Quotient Rule. It applies to a function that is the quotient of two other functions. The formula is:
(f(x) / g(x))’ = (f’(x) g(x) – f(x) g’(x)) / (g(x))^2
Remember these formulas and applying them becomes second nature.
Chain Rule: Deriving Composite Functions
For composite functions, the Chain Rule is your best friend. It’s a way to differentiate a function within another function. This is how it’s done:
- Select the outer function (imagine it as the wrapping of a gift).
- Differentiate the outer function (unwrap the gift).
- Identify the inner function (the gift inside the wrapping).
- Differentiate the inner function (inspect the gift).
- Combine these derivatives as per the Chain Rule formula.
The Chain Rule formula: (f(g(x)))’ = f’(g(x)) g’(x).
Embrace these rules and watch calculus problems untangle before your eyes. Practice regularly and soon, these rules will be your trusted allies in solving calculus challenges.
Deep Dive Into Integration Techniques
Calculus is not just a subject, but a toolkit that helps solve real-world problems. The power of calculus shines through in the form of integration. Here, we will explore the vital techniques of integration, essential for students and professionals alike. These methods turn complex problems into simpler ones.
Indefinite Integrals And Antiderivatives
Indefinite integrals are the reverse of derivatives. They help find functions when given their rates of change. Antiderivatives lead us to the original function before it was differentiated. Let’s look at a basic example:
∫ x dx = 1/2 x2 + C
In this equation, C represents a constant because integrating can produce many functions that differ by a constant.
Methods Of Integration: Substitution And Integration By Parts
Substitution is like a puzzle where you replace parts to make the integral simpler. It often works well with chain rule derivatives.
Integration by parts is a handy method based on the product rule for derivatives. It splits an integral into two parts, as the name suggests. The formula ∫udv = uv – ∫vdu is the key to crack this technique.
- Choose u and dv: Pick wisely to simplify the integral
- Compute du and v: Differentiate u and integrate dv
- Apply the formula: Put all pieces into the integration by parts formula
Definite Integrals And The Fundamental Theorem Of Calculus
Definite integrals have limits and tell the area under a curve. These are key in physics and engineering to calculate work, energy, and more.
| Function | Area from a to b |
|---|---|
| f(x) | ∫ab f(x) dx |
The Fundamental Theorem of Calculus links differentiation and integration. It has two parts:
- Every continuous function has an antiderivative.
- It provides a method to evaluate definite integrals.
It states that if F is an antiderivative of function f on an interval [a, b], then:
∫ab f(x) dx = F(b) - F(a)
This theorem turns the tough task of finding the area under a curve into a simple subtraction problem.
Applications Of Calculus In Various Fields
The elegance of calculus lies in its vast range of applications. This field is not just a staple of pure mathematics. It is instrumental across multiple disciplines. It weaves through various real-world problems, offering solutions that push innovation forward. From engineering marvels to the intricate workings of biological systems, calculus is a silent but powerful force. It is equally pivotal in today’s digital revolution, supporting advancements in technology and artificial intelligence.
Calculus In Engineering And Physics
Engineering and physics find a common language in calculus. It’s a tool that answers complex questions and solves challenging problems. Applications include:
- Designing bridges to withstand stress using integral calculus.
- Computing rocket trajectories with differential equations.
- Predicting electric circuit behavior in electrical engineering.
Contributions Of Calculus To Economics And Biology
Calculus extends its reach to economics and biology, revealing patterns and changes:
| Economics | Biology |
|---|---|
| Understanding market dynamics with cost functions. | Modeling population growth using rate of change. |
| Maximizing profits through optimization problems. | Analyzing enzyme reactions in biochemistry. |
Innovative Uses Of Calculus In Computer Science And Ai
In the realm of computer science and AI, calculus proves indispensable:
- Algorithms optimization hinges on calculus principles.
- Machine learning models train using calculus-based methods.
- Graphics generated by computers use calculus for 3D renderings.
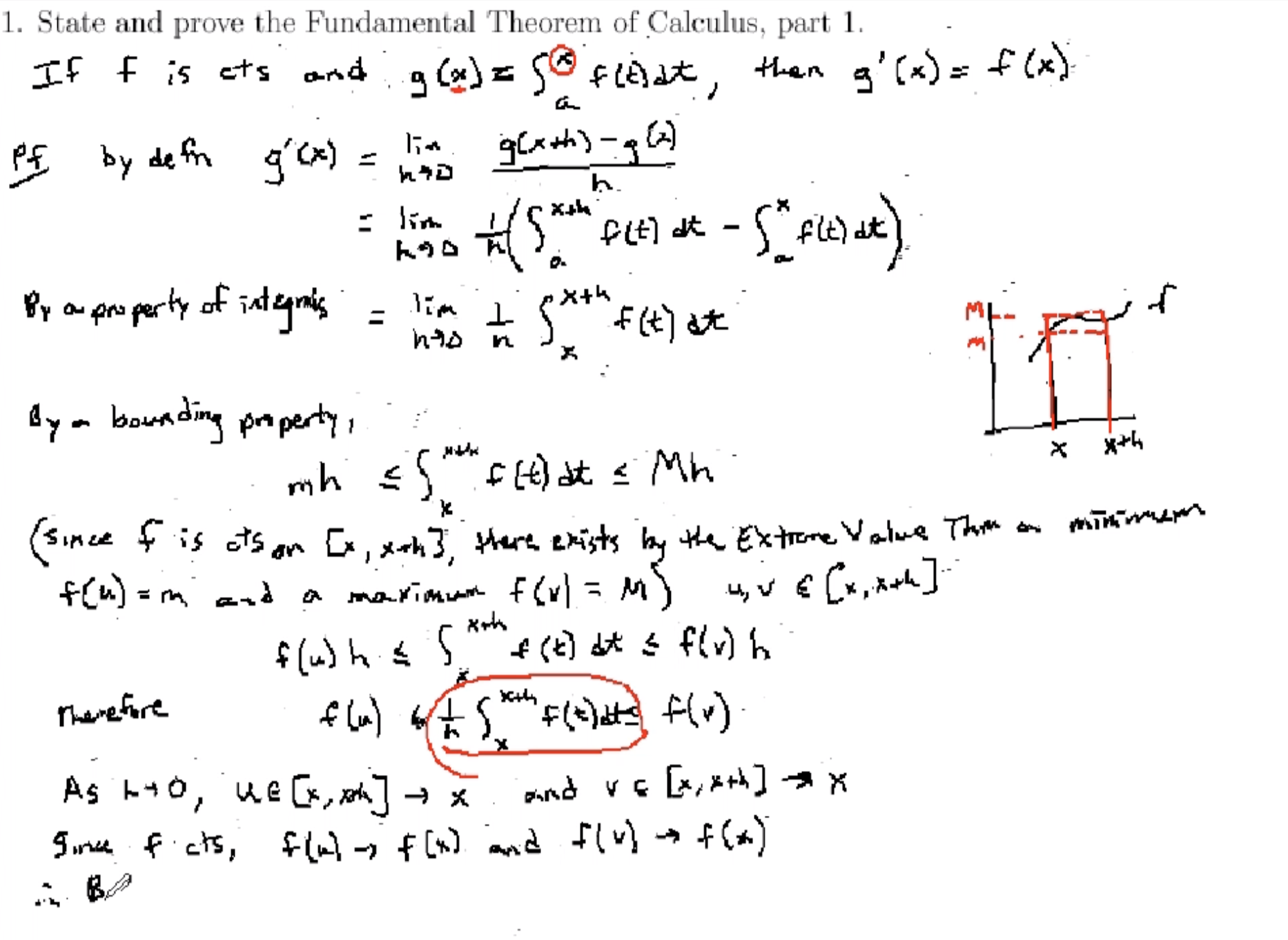
Credit: vmlc.tamu.edu
The Role Of Calculus In Modern Technology
Think about your smartphone, the weather forecast, or your favorite video game. All these wonders exist thanks to calculus. Calculus is the mathematics of change and motion, and it plays a crucial role in driving innovation and building the technology we rely on every day. It powers some of the most advanced systems, solving problems from predicting trends to designing complex structures. Let’s explore how calculus shapes the technology transforming our world.
Improving Machine Learning With Calculus
Machine learning algorithms learn from data to make accurate predictions and decisions. Calculus, specifically differential calculus, is fundamental here. It helps optimize algorithms by finding the minimum and maximum points of functions — basically fine-tuning a machine’s brain. This magic behind your phone recognizing your face or a car driving itself is thanks to calculus in action.
Simulation And Modeling Of Natural Phenomena
Calculus enables us to simulate real-world phenomena. Be it the rolling waves of the ocean or the growth of a population, these simulations rely on calculus-based equations. Meteorologists use it for weather predictions while architects apply it to model airflow around buildings. Simulating reality so precisely allows for safer designs and better planning, saving time and money.
Optimization Problems In Engineering And Research
In engineering and research, calculus is key to solving optimization problems. Whether it’s reducing waste in manufacturing or improving fuel efficiency in cars, calculus finds the best solutions. Engineers use calculus to identify the optimal design parameters within constraints to enhance performance and efficiency in projects ranging from bridges to renewable energy systems.
Advanced Topics In Calculus
As you journey deeper into the world of calculus, you’ll discover that it extends far beyond basic derivatives and integrals. Advanced calculus opens up new dimensions and dynamic systems that describe our complex world. Let’s unpack these sophisticated areas.
Multivariable Calculus: Beyond One Dimension
Multivariable calculus takes you into the realm of several dimensions. Here, you learn to solve puzzles with multiple unknowns.
- Partial Derivatives – Slice through functions for each variable.
- Multiple Integrals – Capture volumes under surfaces in 3D space.
- Gradient – Navigate the steepest slopes of curves.
Imagine climbing a mountain with different paths. Here’s the table of contents for Multivariable Calculus:
| Chapter | Topic |
|---|---|
| 1 | Functions of Several Variables |
| 2 | Vector-Valued Functions |
| 3 | Partial Derivatives & Extrema |
Differential Equations: Describing Dynamic Systems
In differential equations, you learn how to sketch the growth of populations or the sway of pendulums.
- Ordinary Differential Equations (ODEs) – Equations with one variable that involve derivatives.
- Partial Differential Equations (PDEs) – Equations with several variables and partial derivatives.
Think of it as coding the rules for nature’s behaviors.
Vector Calculus: Calculus In Multiple Dimensions
Vector calculus takes the leap into spaces with more than three dimensions. We explore new tools for these dimensions.
- Divergence – Measures source strength in fields.
- Curl – Detects rotation in fields.
- Line and Surface Integras – Adds up values along paths or over areas.
This subject lets us peer into the universe’s complex machinery, where every force and motion plays a role.

Credit: www.insidehighered.com
Understanding Infinity: Series And Sequences
Welcome to the intriguing world of Calculus where we unlock the mysteries of infinity with Series and Sequences. These mathematical concepts are not just symbols on paper—they shape the foundation of how we understand growth, motion, and the nature of the universe. Let’s dive deep into their intriguing aspects.
Convergent And Divergent Series: Defining Infinity
Imagine adding numbers forever. Will they reach a limit or continue endlessly? This is where Convergent and Divergent Series come into play.
- Convergent Series settle down to a single value as you add more terms.
- Divergent Series keep growing or oscillating without approaching a specific value.
A classic example is the Geometric Series. For a ratio between -1 and 1, it converges.
Here’s a simple visual:
| Series | Converges/Diverges? | Example |
|---|---|---|
| 1/2 + 1/4 + 1/8 + … | Converges | Sum = 1 |
| 1 + 1 + 1 + … | Diverges | No Limit |
Power Series And Taylor Expansions: Approximating Functions
Functions shape our world, from simple slopes to complex waves. But some are too tough to handle. Enter Power Series and Taylor Expansions.
These powerful tools turn complex functions into simple polynomials. Think of them as math’s version of a recipe. With just the right ingredients—the function’s derivatives at a point—you can cook up an approximation.
Here’s a peek at a Power Series:
f(x) = a0 + a1x + a2x^2 + a3x^3 + ...
And a special case, the Taylor Expansion, for function f centered at x=c looks like:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + ...
Fourier Series: Decomposing Periodic Functions
Every repeating pattern, from the tides to our heartbeats, is a periodic function. And Fourier Series can break them down like a music composer splitting a harmony into notes.
Fourier Series express periodic functions as the sum of sine and cosine waves, each having different frequencies. This decomposition highlights the different ‘notes’ that make up the complete function.
Here is the form of a Fourier Series:
f(x) = a0 + ∑(an cos(nωx) + bn sin(nωx))
In this equation, an and bn are the amplitudes of the cosine and sine waves, respectively, and ω is the fundamental frequency.
Mathematicians and engineers use these to analyze and reconstruct signals in fields like acoustics, electronics, and even image processing.
Challenges And Misconceptions In Learning Calculus
Calculus can seem like a mountain to climb for many students, with complex theories and a web of applications. This section examines the common roadblocks learners face and the myths that persist around calculus. Furthermore, insights will be shared on effective teaching strategies and appropriate mindset to foster calculus mastery.
Common Difficulties And How To Overcome Them
Understanding calculus requires time and patience. Many students struggle with fundamentals such as limits, derivatives, and integrals.
- Grasping abstract concepts: Use real-world examples to make ideas clearer.
- Complex calculations: Practice regularly to improve speed and accuracy.
- Linking different topics: Create mind maps to see how concepts connect.
Building a solid foundation in precalculus skills is also crucial for success. This means focusing on algebra, geometry, and trigonometry.
Dispelling Myths And Building A Strong Conceptual Framework
Many misconceptions can hinder the learning process in calculus.
| Myth | Reality |
|---|---|
| Calculus is only for geniuses. | With dedication, anyone can understand calculus. |
| It has no real use. | Calculus applications are everywhere, from medicine to economics. |
To overcome these myths, students should engage with calculus actively by solving problems and applying concepts in experiments.
Strategies For Teaching And Communicating Complex Ideas
The key to teaching calculus lies in clear communication and interactive learning.
- Break down complex problems into simpler, more manageable parts.
- Encourage questions to ensure students understand before moving on.
- Utilize technology: Interactive tools can bring calculus to life.
Teachers can inspire students by demonstrating how calculus shapes the world, thereby nurturing a genuine interest and curiosity in the subject matter.

Credit: www.reddit.com
The Future Of Calculus Education
The Future of Calculus Education promises exciting advancements in how students engage with this essential mathematical field. As educational methods evolve, calculus teaching is slated to transform, becoming more interactive, accessible, and aligned with the needs of modern learners. Let’s explore how the next generation will crack complex derivatives and master integrals with the aid of technological and pedagogical innovation.
Innovations In Online Learning And Interactive Resources
Technological growth has dramatically shaped online education. Future calculus courses will likely feature virtual reality (VR) environments, where students can visualize 3D mathematical concepts. Additionally, adaptive learning platforms will provide tailored assistance to help every learner excel. Key innovations include:
- Customized learning paths that adapt to individual paces and styles.
- Immediate feedback loops, refining understanding in real-time.
- Collaborative tools that foster group study and peer-to-peer learning.
The Impact Of Educational Research On Calculus Pedagogy
Educational research continues to unveil better teaching methods for calculus. Research outcomes direct curriculum designers to integrate strategies that enhance comprehension. Crucial developments include:
- Problem-based learning that encourages analytical thinking.
- Inclusion of real-world scenarios making calculus relevant.
- Focus on conceptual understanding over memorization.
Preparing For Emerging Fields: The Next Frontier In Calculus
The future of calculus also demands preparing students for interdisciplinary applications. Calculus education will be the foundation for careers in data science, artificial intelligence, and modeling. To stay ahead of the curve, curriculums might feature:
| Emerging Fields | Calculus Applications |
|---|---|
| Data Science | Statistical analysis and predictive modeling |
| Artificial Intelligence | Algorithm development and optimization |
| Environmental Modeling | Climate change projections and resource management |
This integration ensures that calculus stays relevant and powerful, enabling innovative breakthroughs across sectors.
Conclusion
Calculus stands as the cornerstone of modern mathematics and science. Its principles guide engineers, scientists, and economists. Embracing its concepts unlocks a world of problem-solving potential. So, dive into the beauty of calculus, and let it sharpen your analytical prowess for a sharper mind and a brighter future.